Projects
Multiresolutions Aeroacoustic Simulations
Numerical simulations aim to represent the real-world dynamics of a physical system with the help of a computer. Despite being an incredibly complex machine, a computer is, at its core, an ultra-fast calculator with increasing but finite capacity. In contrast, real-world systems are infinite: whatever level of zooming you look at, one always finds that space is continuous. The mathematical modeling alleviates this issue in its final steps by considering only slices of space (and time). The number of slices chosen or the resolution is then directly related to the accuracy of the model. Unfortunately, the resolution can not be arbitrarily high as it will increase the computational effort and ultimately exceed the capacity of the computer. It may be desirable to have a fine resolution where a phenomenon is of interest and a coarse resolution elsewhere to decrease the cost of the simulation. The computational domain is then composed of multiple subdomains of different resolutions.
The main difficulty is how correctly exchange information between these subdomains and reconstruct missing data. An inadequate transition between two resolutions in computational fluid dynamics simulations results in the emission of a pressure wave or equivalently a spurious (non-physical) acoustic noise.
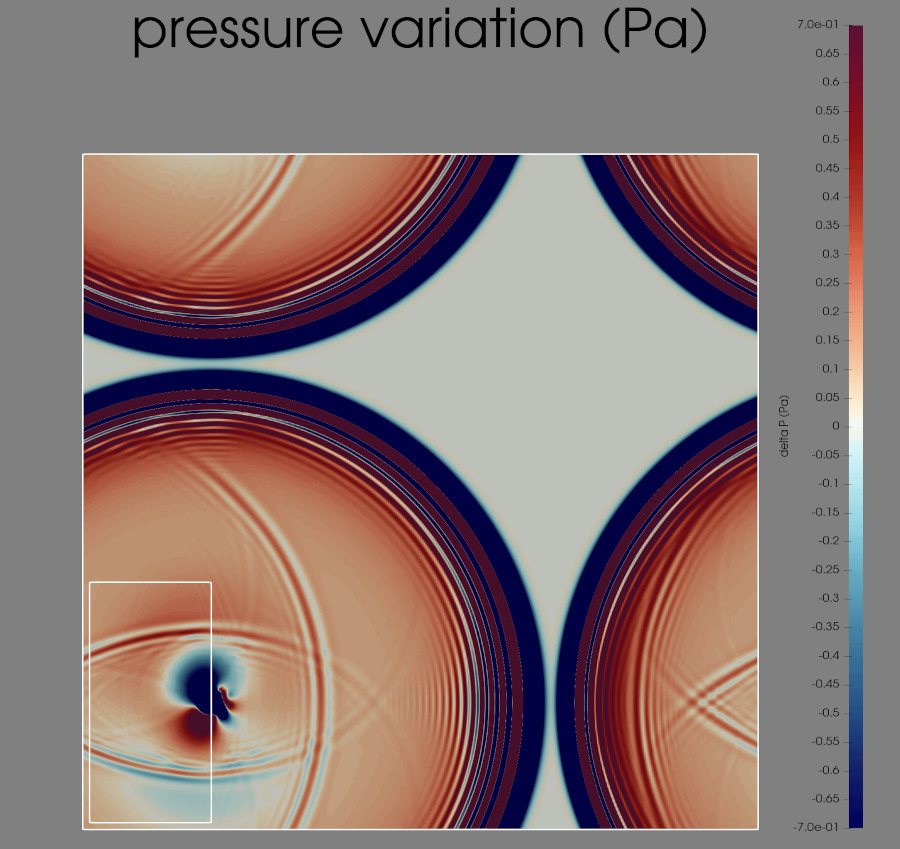
The white lines in the previous image denote the grid transitions. A small patch of a finer resolution is embedded in a two-dimensional domain. Initially at its center, a vortex corresponding to a depression of \(7000\)Pa moves from the left to the right. Multiple concentric pressure waves caused by the initial conditions are visible. In this image, the vortex is approximately crossing the transition between two resolutions (from fine to coarse). The circular shape of the vortex is negligibly affected by the grid transition. Nonetheless, two pressure-wave of magnitude \(\pm0.7\)Pa are emitted behind the vortex, which is equivalent to an error of \(0.01\\%\) relative to the vortex magnitude. Reducing this error is of paramount importance for aero-acoustic simulations to obtain accurate results.
Lucien Vienne acknowledges the funding of the French DGAC under the project OMEGA3. My work carried out during my post-doc at LMFA was part of a scientific collaboration including CS-group, Renault, Airbus, École Centrale de Lyon, CNRS, and Aix-Marseille University.
Viscous Fingering Instability
Viscous fingering is an ubiquitous instability that occurs when a less viscous fluid displaces a more viscous fluid in a porous medium. The interface between the two fluids starts to deform, and finger-like patterns emerge and grow. This phenomenon can either increases the mixing in porous media, which is incredibly difficult because of the absence of turbulence that can actively stir the flow or be dramatic to some processes.
The typical example is secondary oil recovery, for which fingering from the injected aqueous solution pushing the more viscous oil in underground reservoirs of porous rocks reduces the sweep efficiency severely. Similarly, one solution to decrease the carbon dioxide emitted to the atmosphere is to capture it directly from the power plants and gas production sites, and stores in available reservoirs. The interaction between the supercritical \(\text{CO}_2\) and the interstitial fluids, usually brine, is of interest. The resulting mixture from the carbon dioxide dissolution could undergo fingering and change radically the distribution of \(\text{CO}_2\) in the reservoir. Viscous fingering is also detrimental in the case of chromatography, a technique used to separate and identify chemical compounds in a mixture flowing through a porous medium. The displacing fluid (the eluent) may be less viscous than the sample mixture. The initial planar interface will deform because of fingering, resulting in an inefficient separation. Last, viscous fingering can play a major role in soil contamination by enlarging considerably the polluted area. Hence the study of viscous fingering is essential in numbers of domains.

In my PhD project, I simulate the viscous fingering instability using the lattice Boltzmann method. The previous picture shows the evolution of the molar fraction of a binary mixture. The core ingredients of the instability are the diffusion and the viscosity contrast between the species. The behavior of the instability can dramatically change for a mixture of three and more species compared to the binary case. For instance, viscous fingering could be induced by reverse diffusion despite having a stable initial flow configuration.
Multicomponent Flows
In nature, chemical compounds commonly mix each other. One of the elemental material in fluid mechanics, air, is predominantly composed of two components: nitrogen (\(\text{N}_2\), \(\approx 78\%\)) and oxygen (\(\text{0}_2\), \(\approx 21\%\)). Mass transfer seems at first sight not something too complicated: a species should move down its concentration gradient. This is known as the first Fick's law, which can be written for two components as
The flux of the first species is proportional to its concentration gradient according to the coefficient of diffusion \(\mathcal{D}\). However, this approach to mass transfer for a mixture of three and more components is inadequate1, and unexpected behavior can occur as in the case of the Loschmidt's experience2. Consider two tubes of the same dimension each filled with a mixture (argon methane hydrogen or \(\text{Ar}\ \text{CH}_4\ \text{H}_2\)) of a different composition. The left and right tubes are joined at the beginning of the experiment, then the left and right mean compositions are measured in time during the mixing as plotted in the figure below.
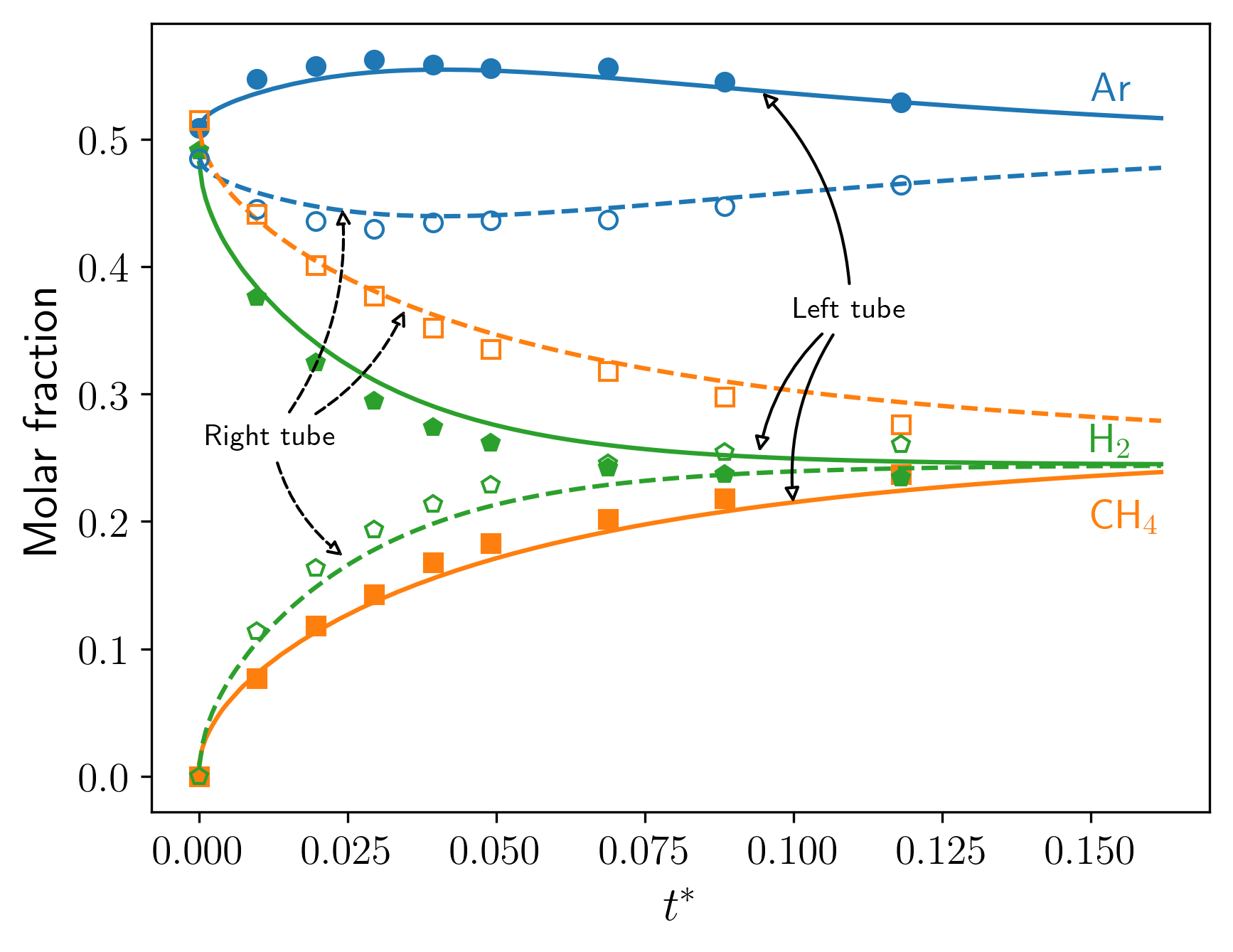
As expected, the hydrogen and methane diffuse in the opposite direction of their concentration gradient, but the argon exhibits a non-standard behavior. The argon diffuses in the same direction of its own concentration gradient: from the right tube to the left tube, i.e., from the low concentration to the high concentration! After, the concentration of argon reaches a plateau and does not evolve even in the presence of a fairly large concentration gradient between the two tubes. The reverse diffusion, diffusion barrier phenomena, and osmotic diffusion (diffusion even with a null concentration gradient, not present here) are specific to the mixing of three and more components. Finally, the concentration in both tubes slowly tends towards the same value.
Forgetting about Fick's law, it is easy to physically interpret what is happening. The hydrogen diffuses to the other tube because there is far more hydrogen in the right tube than in the left tube, indeed the random thermal motions will on average cause the hydrogen to move to the less populated tube. Methane is also subject to the same mechanism. On the contrary, at some points, the argon seems to be dragged by the methane. There is actually more friction between the heavy molecules of methane and argon than between the light molecules of hydrogen and argon. In consequence, the diffusion of argon is at some point governed by the concentration gradients of hydrogen and methane, rather than its own concentration gradient, which is relatively small. Note that using a different initial mixture composition, the reverse diffusion phenomena could also occur with the methane instead of argon.
The Maxwell-Stefan approach to mass transfer is more appropriate than Fick's law for the diffusion of three and more components. Further details can be found in the third chapter of my PhD thesis. In multi-component flows, molecular diffusion and viscous dissipation play an important role in the dynamic of the mixing. See publications section for further details.