Multi-component flows
In nature, chemical compounds commonly mix each other. One of the elemental material in fluid mechanics, air, is predominantly composed of two components: nitrogen ($\text{N}_2$, $\approx 78\%$) and oxygen ($\text{0}_2$, $\approx 21\%$). Mass transfer seems at first sight not something too complicated: a species should move down its concentration gradient. This is known as the first Fick’s law, which can be written for two components as
$$ \mathbf{J}_1=-\mathcal{D}\frac{dc_1}{dz}, ~ \text{and } J_2=-J_1$$
The flux of the first species is proportional to its concentration gradient according to the coefficient of diffusion $\mathcal{D}$. However, this approach to mass transfer for a mixture of three and more components is inadequate1, and unexpected behavior can occur as in the case of the Loschmidt’s experience2. Consider two tubes of the same dimension each filled with a mixture (argon methane hydrogen or $\text{Ar}\ \text{CH}_4\ \text{H}_2$) of a different composition. The left and right tubes are joined at the beginning of the experiment, then the left and right mean compositions are measured in time during the mixing as plotted in the figure below.
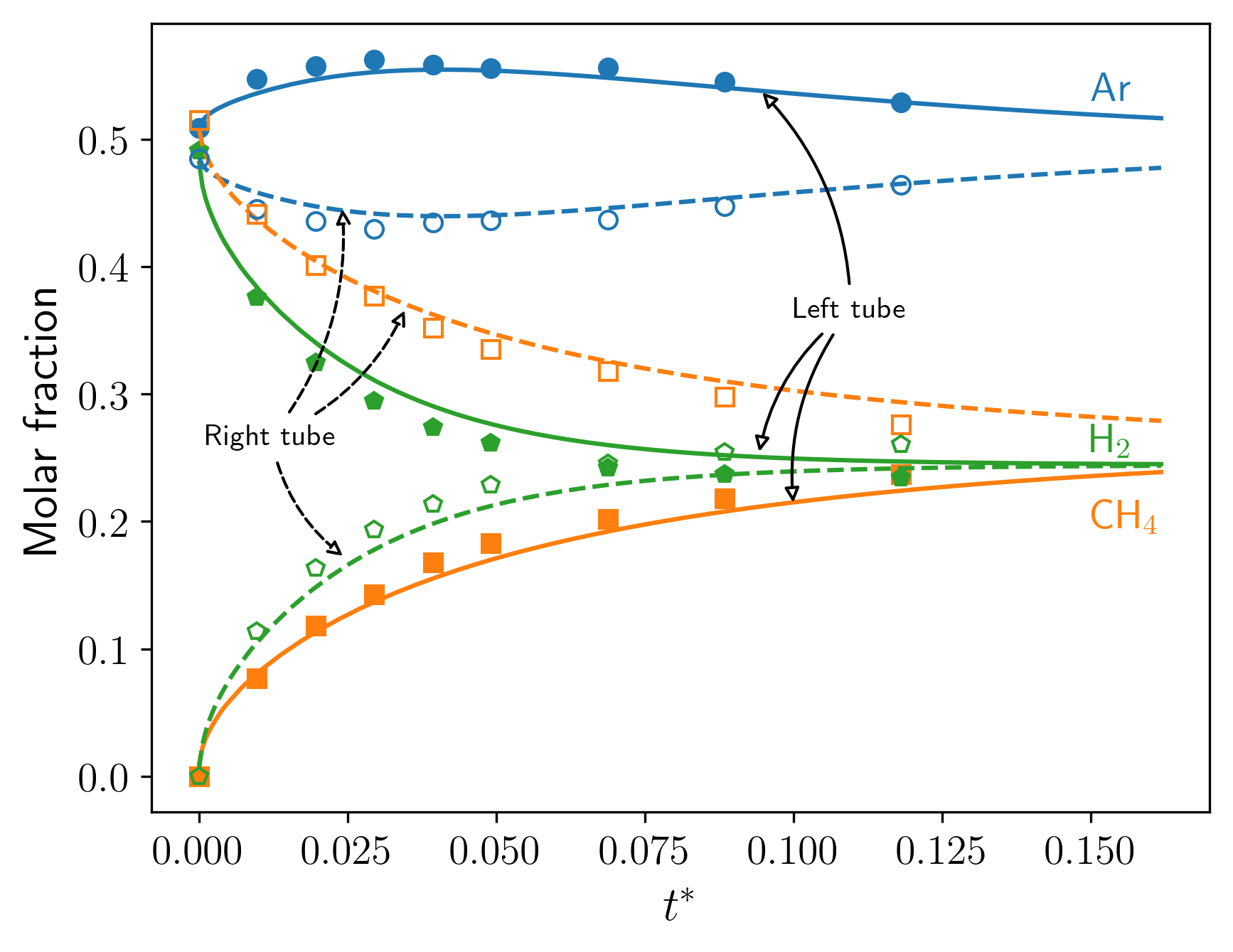
As expected, the hydrogen and methane diffuse in the opposite direction of their concentration gradient, but the argon exhibits a non-standard behavior. The argon diffuses in the same direction of its own concentration gradient: from the right tube to the left tube, i.e., from the low concentration to the high concentration! After, the concentration of argon reaches a plateau and does not evolve even in the presence of a fairly large concentration gradient between the two tubes. The reverse diffusion, diffusion barrier phenomena, and osmotic diffusion (diffusion even with a null concentration gradient, not present here) are specific to the mixing of three and more components. Finally, the concentration in both tubes slowly tends towards the same value.
Forgetting about Fick’s law, it is easy to physically interpret what is happening. The hydrogen diffuses to the other tube because there is far more hydrogen in the right tube than in the left tube, indeed the random thermal motions will on average cause the hydrogen to move to the less populated tube. Methane is also subject to the same mechanism. On the contrary, at some points, the argon seems to be dragged by the methane. There is actually more friction between the heavy molecules of methane and argon than between the light molecules of hydrogen and argon. In consequence, the diffusion of argon is at some point governed by the concentration gradients of hydrogen and methane, rather than its own concentration gradient, which is relatively small. Note that using a different initial mixture composition, the reverse diffusion phenomena could also occur with the methane instead of argon.
The Maxwell-Stefan approach to mass transfer is more appropriate than Fick’s law for the diffusion of three and more components. Curious? Further details can be found in the third chapter of my PhD thesis.
In multi-component flows, molecular diffusion and viscous dissipation play an important role in the dynamic of the mixing. In an article, I propose a lattice Boltzmann method for miscible gases.